大涡模拟不仅对网格的解析度有要求,而且对网格质量也有更高的要求。本文介绍一种由网格带来的误差,commutation error,并简单分析其对结果的影响。
在 LES 模拟的程序中,常用的一种过滤方法是隐式过滤,即,用当地网格的尺度作为该处的过滤尺度。这种方法在各种类型的网格上实现起来都相对简单。只是,稍微复杂一点的几何构体,生成的网格的尺度总是不可能一样,这也就意味着过滤尺度是变化的。如果相邻网格的尺度变化很大,这也将引起相邻网格的过滤尺度相差很大,这时就会带来严重的 commutation error。
Commutation error 产生的根本原因是,当相邻网格过滤尺度不一样时,,$\overline{\tfrac{\partial \phi}{\partial x}} \neq \tfrac{\partial \overline{\phi}}{\partial x}$。下面举一个例子来说明:
假设有一个场量,解析值为
$$
\phi = 1-x^2
$$
其导数为
$$
\frac{\partial \phi}{\partial x} = -2x
$$
在一个如下图的网格中来进行过滤
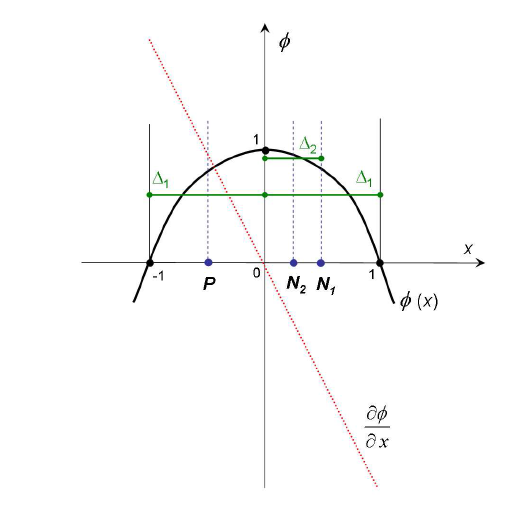
第一次,我们对点 $P$ 和 $N_1$ 处进行过滤,过滤直径都是 $\Delta_1 = 1$,使用 top hat 过滤函数,即
$$
G(x,\Delta)=
\begin{cases}
\frac{1}{\Delta} & if(|x’\le\frac{\Delta}{2}|) \\
0 & otherwise
\end{cases}
$$
则
$$
\overline{\phi}_P = \oint G(x,x\prime;\Delta)\,f(x\prime) dx\prime = \int _{-\infty} ^{-1} 0\cdot \phi(x\prime) dx\prime + \int_{-1}^{0} \frac{1}{\Delta_1} \cdot \phi(x\prime)dx\prime + \int _{0} ^{\infty} 0\cdot \phi(x\prime) dx\prime = \frac{2}{3}
$$
类似地,
$$
\overline{\phi}_{N_1} = \int_0^1 \frac{1}{\Delta_1} \cdot \phi(x\prime) dx\prime = \frac{2}{3}
$$
另一方面,对梯度使用过滤,得
$$
\Bigg(\overline{\frac{\partial \phi}{\partial x}} \Bigg)_0= \int_{-0.5}^{0.5} \frac{1}{\Delta_1}\cdot(-2x)dx = 0
$$
而
$$
\frac{\partial \overline{\phi}}{\partial x} = \frac{\overline{\phi}_{N1}-\overline{\phi}_P}{x_{N1}-x_{P}} = 0
$$
这说明,当相邻网格的过滤尺度一致时,commutation error 为零。但是,当过滤尺度不一致时,考虑右边的网格中心为 $N_2$ 的情形,此时
$$
\overline{\phi}_{N2} = \int_{0}^{0.5} \frac{1}{\Delta_2} \cdot \phi dx = \frac{11}{12}
$$
$$
\frac{\partial \overline{\phi}}{\partial x} = \frac{\overline{\phi}_{N2}-\overline{\phi}_P}{x_{N2}-x_{P}} = \frac{1}{6} \neq 0
$$
这时就产生了 commutation error。
所以,网格尺度不均匀现象严重的区域就会出现显著的 commutation error。边界层是容易出现网格尺度不一致的区域,在壁面上,严格来说,过滤尺度必须是零,否则将破坏无滑移条件。这种情况还可以通过 DES 这样的方法来处理。但是,核心区也可能出现相邻网格不一致的情形。局部网格加密是一种实用的节省计算量的方法,这种方法只需要在重要区域进行加密,不必全局加密。但是局部加密就导致了相邻网格尺度不一致,由此就带来了显著的 commutation error。所以,使用局部加密时,要注意不要让相邻两种等级的网格的边界落在重要区域。
局部加密效应可以从下图看出
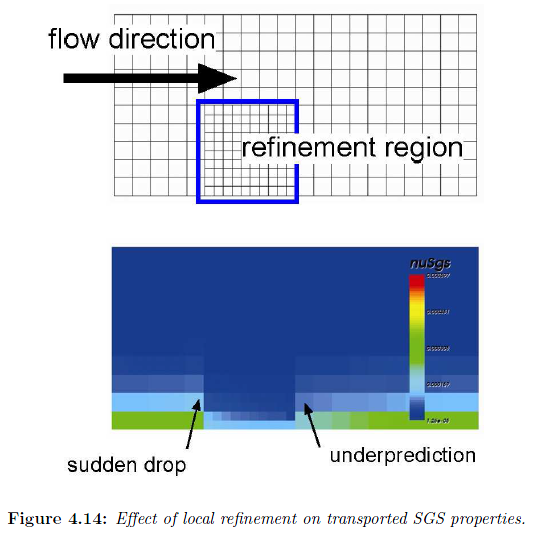
当从细网格向粗网格过渡时,会出现亚格子粘度的突降;当从粗网格过渡到细网格时,亚格子粘度会突然上升。有一种办法是对过滤尺度进行光滑处理:
$$
\Delta P=max(\Delta P, \Delta N/C_{\Delta s})
$$
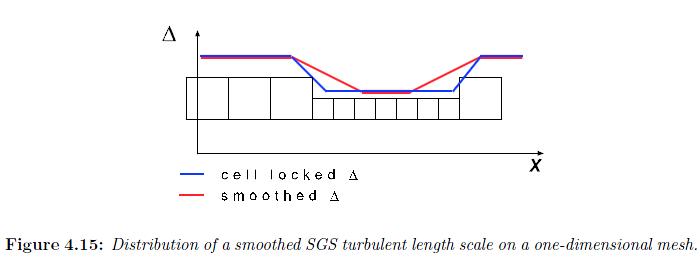
$C_{\Delta s}$ 的取值约为 1.5。
用这种方法可让局部加密带来的问题得到部分缓解。亚格子粘度在粗细网格交接附近的过渡也更光滑。
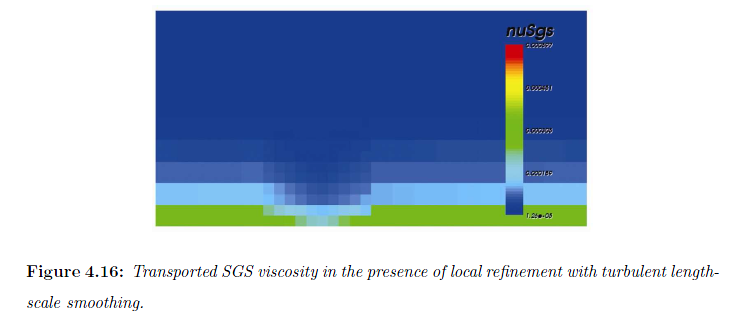
误差总是无可避免的,降低误差的技术也有很多。从“计算性价比”(即为了得到一定准确度的结果所耗费的计算量) 的角度看,没有哪个结果就一定是严格地错误或者正确,只是“计算性价比”不同。有时候为了降低计算量,在一些区域即便产生了严重的误差,也是可以接受的。关键是要对误差差生的原因有清楚的认识,尽量不要让很大的误差出现在重要的区域。
本篇的图,文,公式,完全取材整理自 Eugene de Villiers 的博士论文 “The Potential of Large Eddy Simulation for the Modeling of Wall Bounded Flows”,特此声明。