2016-08-21

OpenFOAM 中求解 ODE 一例

本篇介绍如何编写一个小程序来调用 OpenFOAM 的 ODE 求解器来求解任意常微分方程的初值问题。

1. 数学背景

首先简要看一下涉及的数学背景。对于一阶的常微分方程，
$$
y’=f(x,y), \quad x\in[a,b] \\
y(a)=y_0
$$
常微分方程，如果存在解析解的话，其解应该是一个函数 $y=f(x)$。然而，大多数常微分方程是没有解析解的，只能数值求解。数值方法得到的，是一系列的 $x_0, x_1, \cdots x_n$ 对应的函数值 $y_0, y_1, \cdots y_n$。

常用的数值解法有：

显式欧拉法
这种方法最简单，将区间 $[a,b]$ 分成 n 份，则得到步长 $h=(b-a)/n$。以 $y(a)=y_0$ 为起点，通过下述迭代，
$$
y_{m+1} = y_m+hf(x_m,y_m)
$$
可以得到 $x_m=a+m*h$ 处的函数值 $y_m$，此即为常微分方程的数值解。显式欧拉法形式简单，但是只有一阶精度，而且稳定性是有条件的，一般在实际中较少用到。
改进的欧拉法
这种方法是在显式欧拉法的基础上改进得到，将显式欧拉法中使用的向前积分改为梯形积分。其迭代形式为
$$
y_{m+1} = y_m +\frac{h}{2}[f(x_m,y_m)+f(x_{m+1},y_{m+1})]
$$
这种方法不是显式地，所以，需要在每一步内进行迭代求解。可以用如下的迭代公式
$$
y_{m+1}^{(n+1)} = y_m +\frac{h}{2}[f(x_m,y_m)+f(x_{m+1},y_{m+1}^{(n)})]
$$
注意，这里的 n 指的是计算 $y_{m+1}$ 的值时的内迭代次数，迭代的初始值 $y_{m+1}^{(0)}$ 可以用显式欧拉公式来给出
$$
y_{m+1}^{(0)} = y_m + hf(x_m, y_m)
$$
显式 4 阶 Runge-Kutta 方法
这是现实中常用的一种方法，其迭代形式如下
$$
\begin{align*}
y_{m+1} & = y_m + \frac{h}{6}[k_1+2k_2+2k_3+k_4] \\
k_1 & = f(x_m, y_m) \\
k_2 & = f(x_m+\frac{1}{2}h, y_m+\frac{1}{2}hk_1) \\
k_3 & = f(x_m+\frac{1}{2}h, y_m+\frac{1}{2}hk_2) \\
k_4& = f(x_m+h, y_m+hk_3)
\end{align*}
$$

除了以上，当然还有很多方法，比如预测校正等等，这里就不再逐一介绍了。

问题是，实际中遇到的还可能是高阶的常微分方程，比如，弹簧-谐振子系统可以用以下e二阶常微分方程描述
$$
\frac{d^2y}{dt^2} = -\frac{k}{m}y
$$

高阶常微分方程的初值问题，可以用以下通式来描述
$$
y^{n} = f(x,y,y’,\cdots y^{n-1})
$$

其初始条件为
$$
y(0) = a_0, \quad y’(0) = a_1, \quad \cdots, \quad y^{n-1}(0) = a_n
$$
对于这种高阶常微分方程，可以将其表述为一系列一阶常微分方程的组成的方程组来求解。下面以二阶常微分方程为例，介绍如何将高阶常微分方程的初值问题转化为一阶常微分方程组。
考察如下二阶常微分方程
$$
y’’ = f(x,y,y’), \quad x\in[a,b] \\
y(a) = a_0, \quad y’(a) = a_1
$$

若令 $z=y’$，则上述二阶常微分方程可以表示成如下方程组
$$
\left \{
\begin{align*}
y’ &= z \\
z’ &= f(x,y,z)
\end{align*}
\right. \\
y(a)=a_0,\quad z(a)=a_1
$$

这个方程组，就可以用前面介绍的一阶常微分方程的解法来求解了，比如，若用最简单的显式欧拉法，则
$$
\begin{align*}
y_{m+1} &= y_m + h z_m \\
z_{m+1} &= z_m +hf(x_m, y_m, z_m)
\end{align*}
$$
或者用显式 4 阶 Runge-Kutta 方法
$$
\begin{align*}
y_{m+1} & = y_m + \frac{h}{6}[K_1+2K_2+2K_3+K_4] \\
z_{m+1} & = z_m + \frac{h}{6}[M_1+2M_2+2M_3+K_4] \\
K_1 & = z_m,\quad M_1=f(x_m, y_m, z_m) \\
K_2 & = z_m + \frac{M_1}{2}, \quad M_2 = f(x_m+\frac{h}{2}, y_m+\frac{K_1}{2}, z_m+\frac{M_1}{2})\\
K_3 & = z_m + \frac{M_2}{2},\quad M_3 = f(x_m+\frac{h}{2}, y_m+\frac{K_2}{2}, z_m+\frac{M_2}{2})\\
K_4& = z_m + M_3,\quad M_4=f(x_m+h, y_m+K_3, z_m+M_3)
\end{align*}
$$

二阶以上的常微分方程，除了可以给出初值条件，还可以给出边值条件，比如
$$
y’’ = f(x,y,y’), \quad x\in[a,b] \\
y(a) = \alpha, \quad y(b) = \beta
$$

这种情况下，就无法直接将此方程转化为一阶常微分方程组了。但是，边值问题可以通过一定的方法转换成初值问题，以下给出一种：试射法。
在不知道 $y’(a)$ 的情况下，不妨假设 $y’(a)=\gamma_1$，这样，就得到了一个初值问题
$$
y’’ = f(x,y,y’), \quad x\in[a,b] \\
y(a) = \alpha, \quad y’(a) = \gamma_1
$$
解此初值问题，得到 $y(b)$ 的值 $\beta_1$，并与 $\beta$ 比较，如果误差足够小，则认为假设的 $y’(a)=\gamma_1$ 是合理的。否则，就对 $\gamma_1$ 进行修正，比如令 $\gamma_2 = \tfrac{\beta}{\beta_1}\gamma_1$，然后再以 $y’(a)=\gamma_2$ 为初值，继续求解初值问题。直到得到的初值问题的解$y(b)=\beta_k$ 与 $\beta$ 足够接近为止。

上述方程可以归纳为，将初值问题转化为如下边值问题
$$
y’’ = f(x,y,y’), \quad x\in[a,b] \\
y(a) = \alpha, \quad y’(a) = \gamma_k, k=1,2,\cdots
$$
若记问题 $y_k(x)$ 的解为 $y(x;\gamma_k)$，则 $\gamma_k$ 的理想值应该满足
$$
F(\gamma) = y(b;\gamma)-\beta = 0
$$
这个方程，可以用牛顿迭代法来求解：
$$
\gamma_{k+1} = \gamma_k-\frac{F(\gamma_k)}{F’(\gamma_k)}
$$
其中，$F(\gamma_k)=y(b;\gamma_k)-\beta=\beta_k-\beta$。那么 $F’(\gamma_k)$ 该如何得到呢？根据 $F(\gamma_k)$ 的定义，可以知道 $F’(\gamma_k) = \frac{\partial y(b;\gamma)}{\partial \gamma}\big|_{\gamma=\gamma_k}$，若定义 $W=\frac{\partial y(b;\gamma)}{\partial \gamma}$，则 $F’(\gamma_k)=W(b;\gamma_k)$。

将上述归纳形式的初值问题，对$\gamma$ 求偏导，得
$$
\frac{\partial y’’}{\partial \gamma} = \frac{\partial f(x,y(x;\gamma),y’(x,y’))}{\partial y} \frac{\partial y(x;\gamma)}{\partial \gamma} + \frac{\partial f(x,y(x;\gamma),y’(x,y’))}{\partial y’} \frac{\partial y’(x,y’)}{\partial \gamma}
$$

根据 $W$ 的定义，有
$$
W=\frac{\partial y(x;\gamma)}{\partial \gamma}, W’=\frac{\partial y’(x,y’)}{\partial \gamma}, W’’=\frac{\partial y’’}{\partial \gamma}
$$

于是，可以得到一个关于 $W$ 的二阶常微分方程
$$
W’’=\frac{\partial f(x,y,y’)}{\partial y} W + \frac{\partial f(x,y,y’)}{\partial y’}W’
$$
其定解条件为
$$
W(a)=\frac{\partial y(a;\gamma)}{\partial \gamma}=0, W’(a)=\frac{\partial y’(a;\gamma)}{\partial \gamma}=\frac{\partial \gamma}{\partial \gamma} = 1
$$

这样就构成了一个关于 $W$ 的二阶初值常微分方程。
总结一下，二阶常微分方程的边值问题
$$
y’’ = f(x,y,y’), \quad x\in[a,b] \\
y(a) = \alpha, \quad y(b) = \beta
$$
的求解步骤如下：

假定一个 $\gamma_1$ 值，求解初值问题
$$
y’’ = f(x,y,y’), \quad x\in[a,b] \\
y(a) = \alpha, \quad y’(a) = \gamma_1
$$
然后计算 $F(\gamma_1)=y(b;\gamma_1)$
求解关于 $W$ 的初值问题
$$
W’’=\frac{\partial f(x,y,y’)}{\partial y} W + \frac{\partial f(x,y,y’)}{\partial y’}W’ \\
W(a) = 0, W’(a) = 1
$$
然后计算 $F’(\gamma_1) = W(b;\gamma_1)$。
更新$\gamma$ 的值，
$$
\gamma_2 = \gamma_1-\frac{F(\gamma_1)}{F’(\gamma_1)}
$$
继续迭代，直到最后得到的 $y(b;\gamma_k)$ 与 $\beta$ 足够接近为止。

2. OpenFOAM 中的实现

为了在OpenFOAM中求解一个任意阶常微分方程的初值问题，需要做如下准备。
考虑一个通用形式的常微分方程
$$
y^{n}=f(x,y,y’,\cdots,y^{n-1})
$$
定义
$$
\begin{align*}
y_1 &=y\\
y_2 &=y’\\
y_j &=y^{\,j-1}, \quad j=1,2,\cdots,n
\end{align*}
$$
如果是求解刚性问题的 ODE 求解器，还需要定义 jacobian 矩阵。
令
$$
\begin{align*}
f_1 &=y’=y_2\\
f_j &=y’_{j}=y^{\,j+1}, \quad j=1,2,\cdots,n
\end{align*}
$$
则 jacobian 矩阵
$$
\begin{equation*}
J =
\begin{bmatrix}
\frac{\partial f_1}{\partial y_1} & \frac{\partial f_1}{\partial y_2} &
\cdots &\frac{\partial f_1}{\partial y_n}\\
\frac{\partial f_2}{\partial y_1} & \frac{\partial f_2}{\partial y_2} &
\cdots &\frac{\partial f_2}{\partial y_n}\\
\vdots & \vdots & \ddots & \vdots \\
\frac{\partial f_n}{\partial y_1} & \cdots & \cdots
&\frac{\partial f_n}{\partial y_n}
\end{bmatrix}
\end{equation*}
$$
此外，还需要给出 $f_1, f_2,\cdots,f_n$ 对自变量 $x$ 的偏导数，$\frac{\partial f_1}{\partial x}, \frac{\partial f_2}{\partial x},\cdots,\frac{\partial f_n}{\partial x}$。

下面举一个例子来具体说明。以常微分方程
$$
y’’=2x+2, x\in[0,1] \\
y(0) = 0, y’(0)= 0
$$
为例，需要定义的量为
$$
\begin{align*}
f_1 &=y’=y_2 \\
f_2 &= y’_{2} = 2x+2
\end{align*}
$$

$$
\begin{equation*}
J=
\begin{bmatrix}
0 & 1 \\
0 & 0
\end{bmatrix}
\end{equation*}
$$

$$
\frac{\partial f_1}{\partial x} = 0, \frac{\partial f_2}{\partial x} = 2
$$

求解这个常微分方程的代码如下：

/*********************************************************
Description

d2y/dx2 = ax + b, with a=2, b=2.
initial value: y(0) = 0; y'(0) = 0

analytical solution: y = 1/3*x^3 + x^2;
**********************************************************/

#include "argList.H"
#include "IOmanip.H"
#include "ODESystem.H"
#include "ODESolver.H"

using namespace Foam;

·// * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * //

class myODE2
:
    public ODESystem
{

    const scalar a_; //parameter
    const scalar b_; //parameter


public:

    myODE2(const scalar& a, const scalar& b)
	:ODESystem(),
	a_(a),
	b_(b)
    {}

    label nEqns() const // number of equations, equals to the order of ODE
    {
        return 2;
    }

    void derivatives
    (
        const scalar x,
        const scalarField& y,
        scalarField& dydx
    ) const
    {
        dydx[0] = y[1];         //f1
        dydx[1] = a_*x + b_;    //f2
    }

    void jacobian // optional
    (
        const scalar x,
        const scalarField& y,
        scalarField& dfdx,
        scalarSquareMatrix& dfdy
    ) const
    {
        dfdx[0] = 0.0;        //df1/dx
        dfdx[1] = a_;         //df2/dx

        dfdy[0][0] = 0.0;     //df1/dy1
        dfdy[0][1] = 1.0;     //df1/dy2

        dfdy[1][0] = 0.0;     //df2/dy1
        dfdy[1][1] = 0.0;     //df2/dy2

    }
};


// * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * //
// Main program:

int main(int argc, char *argv[])
{
    argList::validArgs.append("ODESolver");
    argList args(argc, argv);

    const scalar a = 2.0; 
    const scalar b = 2.0; 

    const label n = 100;         //number of steps
    const scalar endTime = 1.0;  //upper bound of the interval

    // Create the ODE system
    myODE2 ode(a, b);

    dictionary dict;
    dict.add("solver", args[1]);

    // Create the selected ODE system solver
    autoPtr<ODESolver> odeSolver = ODESolver::New(ode, dict);

    // Initialise the ODE system fields
    scalar xStart = 0.0;        // lower bound of the interval
    scalar dx = endTime/n;      //step value

    scalarField yStart(ode.nEqns());
    yStart[0] = 0.0; // initial value of y
    yStart[1] = 0.0; // initial value of y'

    scalar dxEst = 0.1;
    scalar xEnd  = 0.0;

    scalarField dyStart(ode.nEqns()); // dyStart[0]=f1, dyStart[1]=f2 ...

    for(label i =0; i<n; i++)
    {
	    xEnd = xStart + dx;
	    ode.derivatives(xStart, yStart, dyStart);
	    odeSolver->solve(xStart, xEnd, yStart, dxEst);
	    xStart = xEnd;
	    Info << xStart << "    " << yStart[0] << endl; // output (x,y) for each dx.
    }

    return 0;
}

编译之后，假设你的可执行程序名为 TestODE，则运行

1	TestODE RKCK45 > log

就得到了数值解。
将数值解与解析解画图如下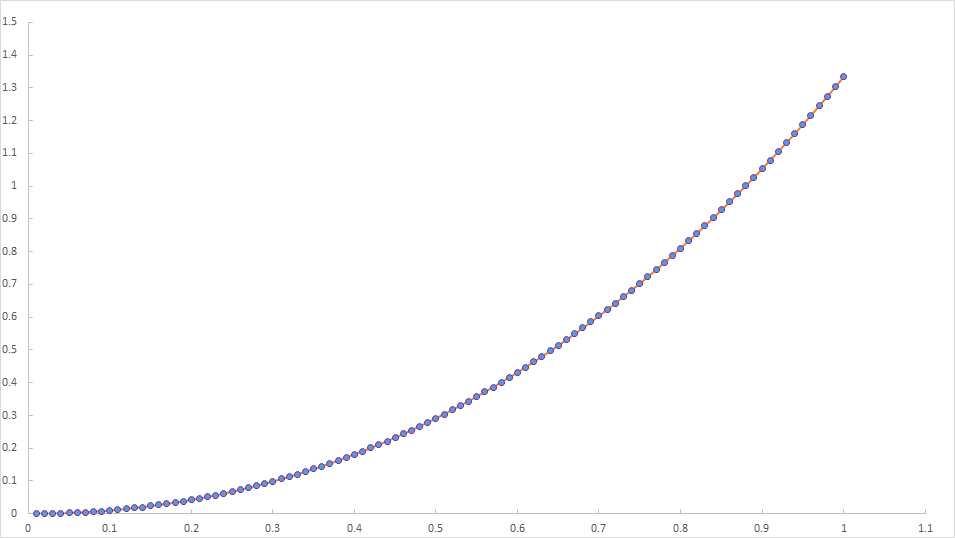

可见在这里简单例子中，数值解与解析解吻合非常好。
同时注意，这个例子，用显式欧拉方法无法得到收敛的解。

参考资料：

http://hassankassem.me/posts/ode/
余德浩 , 汤华中，微分方程数值解法，科学出版社，2003

Giskard's CFD Learning Tricks

CFD and Scientific Computing

OpenFOAM 中求解 ODE 一例

1. 数学背景

2. OpenFOAM 中的实现