本系列分析 OpenFOAM-3.0 版本的湍流模型。从 3.0 版开始,OpenFOAM 中的湍流模型架构发生了较大的变化,其实这种变化在 2.3 版开始已经初露端倪,在 2.3 版里,多相流的湍流模型已经开始跟单相流湍流模型分开。从 3.0 开始,单相流湍流模型和多相流湍流模型统一到了一个架构下。本系列将对 3.0 版的湍流模型进行详细的分析,分为四部分:结构概览,RTS 机制分析,编译新模型的方法,以及一些补充说明。
1. 结构概览
这部分主要是概括一下湍流模型的框架的结构,如下图(请点击右键查看大图):
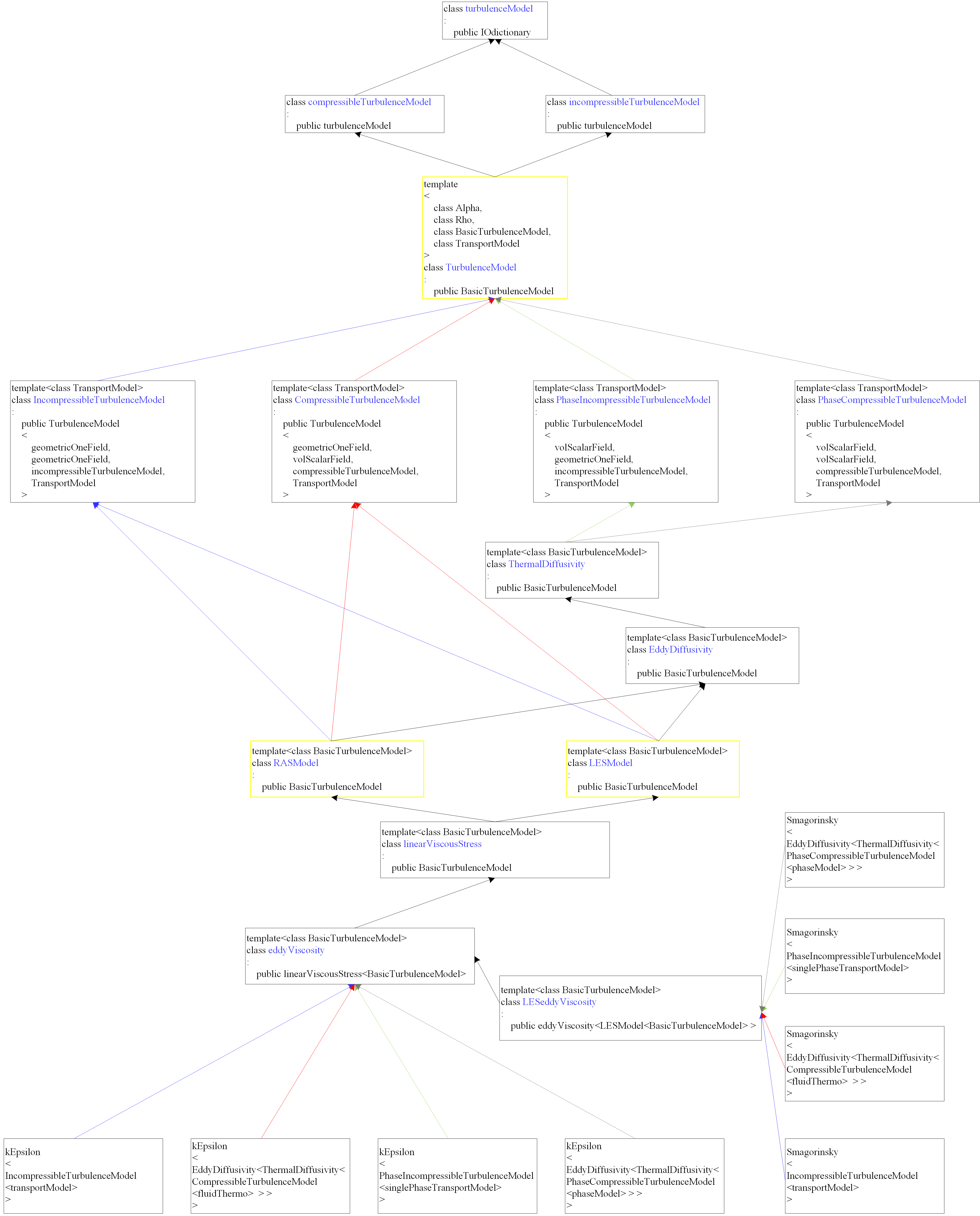
图片中,蓝色字体的是类名,绿框中的类是调用 declareRunTimeSeclectionTable 的类(如果对这个的含义感兴趣,建议参考这篇或者这篇),四种不同颜色的箭头,代表的是四种不同的湍流模型:单相不可压缩湍流模型,单相可压缩湍流模型,多相不可压缩模型,多相可压缩模型。
在图片下面,我用了一个 kEpsilon 和一个 Smagorinsky 模型作为示例,这是因为,这两个湍流模型都是以通用形式来实现的,从 C++ 角度来说,就是模板类。通过代入不同的模板参数, kEpsilon 和 Smagorinsky 这两个模板类可以实例化为不同种类的湍流模型。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47template<class BasicTurbulenceModel>
class kEpsilon
:
public eddyViscosity<RASModel<BasicTurbulenceModel> >
{
// Private Member Functions
// Disallow default bitwise copy construct and assignment
kEpsilon(const kEpsilon&);
kEpsilon& operator=(const kEpsilon&);
......
......
tmp<fvScalarMatrix> epsEqn
(
fvm::ddt(alpha, rho, epsilon_)
+ fvm::div(alphaRhoPhi, epsilon_)
- fvm::laplacian(alpha*rho*DepsilonEff(), epsilon_)
==
C1_*alpha*rho*G*epsilon_/k_
- fvm::SuSp(((2.0/3.0)*C1_ + C3_)*alpha*rho*divU, epsilon_)
- fvm::Sp(C2_*alpha*rho*epsilon_/k_, epsilon_)
+ epsilonSource()
+ fvOptions(alpha, rho, epsilon_)
);
epsEqn().relax();
fvOptions.constrain(epsEqn());
epsEqn().boundaryManipulate(epsilon_.boundaryField());
solve(epsEqn);
fvOptions.correct(epsilon_);
bound(epsilon_, this->epsilonMin_);
// Turbulent kinetic energy equation
tmp<fvScalarMatrix> kEqn
(
fvm::ddt(alpha, rho, k_)
+ fvm::div(alphaRhoPhi, k_)
- fvm::laplacian(alpha*rho*DkEff(), k_)
==
alpha*rho*G
- fvm::SuSp((2.0/3.0)*alpha*rho*divU, k_)
- fvm::Sp(alpha*rho*epsilon_/k_, k_)
+ kSource()
+ fvOptions(alpha, rho, k_)
);
从上述代码可以看出,输运方程中带入了密度 rho 和代表相体积分率的 alpha 。代入不同的模板参数, rho 和 alpha 的取值也会不同,从而实例化为不同的湍流模型,详细的后文还会分析。除此之外,输运方程中还加入了两种源项的实现,一种是以成员函数的形式( epsilonSource() 和 kEpsilon() );另一种是以 fvOptions 的形式,允许用户自定义源项。
在这个架构下,湍流模型是怎么通过 RTS 机制来进行选择的呢?请看下一篇。