OpenFOAM

涡结构提取

为了研究湍流的涡结构，需要有一些方法来将涡结构提取出来，比图在文章中常见类似这种图：
涡结构

本篇介绍怎么在 OpenFOAM 中提取涡结构。

历史上曾用过的涡结构提取有以下几种：

  1. 压强的局部极小值
    在形成涡的地方，通常伴随着压强的极小值。比如:

    这种方法的缺点在于，缺乏客观的压力阈值来捕捉所有的涡结构，而且，压力出现极值的地方不见得就真的有涡。

  2. 流线
    通过流线的封闭来显示涡的结构也是一种常见方法，比如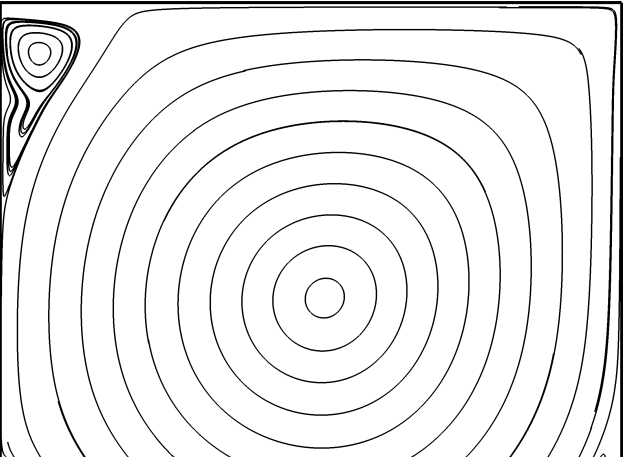

    这种方法有一个最明显的缺点是，流线不满足伽利略不变性，即，如果换一个参考系，则可能显示出来的“涡结构”就完全不一样了。另外，这种方法也难以分辨两个很靠近的涡。

  3. 涡量的模
    用涡量的模来显示涡结构是一种很常用的方法，类似这样

    这种方法在自由剪切流中很有效，不过，对于壁面束缚流动则不太适用，原因是背景流动的剪切性导致的涡量模可以达到跟涡结构处的涡量的模差不多大小，这就使得涡结构难以从背景流动中分离出来了。并且，涡量的模的最大值通常发生在壁面上，而涡的核心显然不可能出现在壁面上。所以这种方法不适合用于提取边界层附近的涡结构。

    OpenFOAM 中提供了两种方法来提取涡结构：Q 和 Lambda2。

  • 速度梯度张量的二阶不变量
    速度梯度 $\nabla \mathbf{U}$ 的二阶不变量 $Q$ 的定义为
    $$
    Q = \frac{1}{2}\Big ( ||\mathbf{W}||^2 - ||\mathbf{S}||^2 \Big )
    $$
    其中
    $$
    \mathbf{W} = \frac{1}{2} \Big ( \nabla \mathbf{U} - (\nabla \mathbf{U}) ^{\mathrm{T}} \Big ) \\
    ||\mathbf{W}|| = (\mathbf{W}:\mathbf{W})^{1/2} \\
    \mathbf{S} = \frac{1}{2} \Big ( \nabla \mathbf{U} + (\nabla \mathbf{U}) ^{\mathrm{T}} \Big ) \\
    ||\mathbf{S}|| = (\mathbf{S}:\mathbf{S})^{1/2}
    $$

可以用 $Q > 0$ 来作为涡结构存在的盘踞。
在 OpenFOAM 中，有一个程序用来计算 $Q$，名字就叫 Q。在流场计算完毕以后，可以运行 Q，然后在 paraview 中显示 Q 值大于 0 的等值面来显示涡的结构。只是，OpenFOAM 中 $Q$ 的计算用的是另一种方法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
//Q.C 
volTensorField gradU(fvc::grad(U));

volScalarField Q
(
    IOobject
    (
        "Q",
        runTime.timeName(),
        mesh,
        IOobject::NO_READ,
        IOobject::NO_WRITE
    ),
    0.5*(sqr(tr(gradU)) - tr(((gradU)&(gradU))))
);

代码里注释说这是另一种计算 $Q$ 的方法，与上面公式的计算方法差别很小。

  • 张量 $\mathbf{W} \cdot \mathbf{W} + \mathbf{S} \cdot \mathbf{S}$ 的第二大特征值

另一种判据是 $\mathbf{W} \cdot \mathbf{W} + \mathbf{S} \cdot \mathbf{S}$ 的第二大特征值 $\lambda _ 2 < 0$。
在 OpenFOAM 中有一个程序用来计算 $\lambda _ 2$ ：Lambda2。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
//Lambda2.C
 const volTensorField gradU(fvc::grad(U));

        volTensorField SSplusWW
        (
            (symm(gradU) & symm(gradU)) + (skew(gradU) & skew(gradU))
        );

        volScalarField Lambda2
        (
            IOobject
            (
                "Lambda2",
                runTime.timeName(),
                mesh,
                IOobject::NO_READ,
                IOobject::NO_WRITE
            ),
            -eigenValues(SSplusWW)().component(vector::Y)
        );

        Info<< "    Writing -Lambda2" << endl;
        Lambda2.write();

注意，OpenFOAM 返回的是 $- \lambda _ 2$，所以，在计算了 Lambda2 后，需要通过 Lambda2 大于 0 的等值面来显示涡结构。本篇开头第一张图片，显示的是圆柱绕流的 Lambda2 = 500 等值面。

参考
Eugene de Villiers, The Potential of Large Eddy Simulation for the Modeling of Wall Bounded Flows, Ph.D Thesis, Imperial College of Science, 2005.