2016-04-02

OpenFOAM 中的边界条件（三）

OpenFOAM 中有很多复杂的边界都是继承自上篇中提到的三个基础边界条件，这些边界条件的代码在上一篇的基础上就很容易看懂了。只不过，还有一些边界条件，不是继承自这三个基础边界条件的，其中有一些都直接或间接继承自另一个重要的边界条件： transformFvPatchField。本篇来看看这个 transformFvPatchField 以及几个继承自它的边界条件。

5. transform

这是一个抽象基类，主要注意一下四个函数的定义：

template<class Type>
tmp<Field<Type> > transformFvPatchField<Type>::valueInternalCoeffs
(
    const tmp<scalarField>&
) const
{
    return pTraits<Type>::one - snGradTransformDiag();
}

template<class Type>
tmp<Field<Type> > transformFvPatchField<Type>::valueBoundaryCoeffs
(
    const tmp<scalarField>&
) const
{
    return
        *this
      - cmptMultiply
        (
            valueInternalCoeffs(this->patch().weights()),
            this->patchInternalField()
        );
}

template<class Type>
tmp<Field<Type> > transformFvPatchField<Type>::gradientInternalCoeffs() const
{
    return -this->patch().deltaCoeffs()*snGradTransformDiag();
}

template<class Type>
tmp<Field<Type> > transformFvPatchField<Type>::gradientBoundaryCoeffs() const
{
    return
        snGrad()
      - cmptMultiply(gradientInternalCoeffs(), this->patchInternalField());
}

由于 snGrad 和 snGradTransformDiag 都是纯虚函数，所以这四个函数的具体返回值需要在派生类中实现了 snGrad 和 snGradTransformDiag 之后才能确定。
另外注意，当模板参数为 scalar 时， gradientInternalCoeffs 函数有特殊的定义：

template<>
tmp<scalarField > transformFvPatchField<scalar>::gradientInternalCoeffs() const
{
    return tmp<scalarField >(new scalarField(size(), 0.0));
}

6. directionMixed

这个类，跟前面的 mixed 有点类似，但是又继承自 transform ，所以，似乎是二者的结合。

template<class Type>
class directionMixedFvPatchField
:
    public transformFvPatchField<Type>
{
    // Private data

        //- Value field
        Field<Type> refValue_;

        //- Normal gradient field
        Field<Type> refGrad_;

        //- Fraction (0-1) of value used for boundary condition
        symmTensorField valueFraction_;

与 mixed 相似之处是，这里也定义了 refValue_ ， refGrad_ 和 valueFraction_ 三个参数，所不同的是，这里的 valueFraction_ 是一个对称张量。

接下来， directionMixed 定义了 snGrad 和 snGradTransformDiag 这两个函数

snGrad 和 snGradTransformDiag

template<class Type>
Foam::tmp<Foam::Field<Type> >
Foam::directionMixedFvPatchField<Type>::snGrad() const
{
    const Field<Type> pif(this->patchInternalField());

    tmp<Field<Type> > normalValue = transform(valueFraction_, refValue_);

    tmp<Field<Type> > gradValue = pif + refGrad_/this->patch().deltaCoeffs();

    tmp<Field<Type> > transformGradValue =
        transform(I - valueFraction_, gradValue);

    return
        (normalValue + transformGradValue - pif)*
        this->patch().deltaCoeffs();
}

template<class Type>
Foam::tmp<Foam::Field<Type> >
Foam::directionMixedFvPatchField<Type>::snGradTransformDiag() const
{
    vectorField diag(valueFraction_.size());

    diag.replace
    (
        vector::X,
        sqrt(mag(valueFraction_.component(symmTensor::XX)))
    );
    diag.replace
    (
        vector::Y,
        sqrt(mag(valueFraction_.component(symmTensor::YY)))
    );
    diag.replace
    (
        vector::Z,
        sqrt(mag(valueFraction_.component(symmTensor::ZZ)))
    );

    return transformFieldMask<Type>(pow<vector, pTraits<Type>::rank>(diag));
}

evaluate 函数

template<class Type>
void Foam::directionMixedFvPatchField<Type>::evaluate(const Pstream::commsTypes)
{
    if (!this->updated())
    {
        this->updateCoeffs();
    }

    tmp<Field<Type> > normalValue = transform(valueFraction_, refValue_);

    tmp<Field<Type> > gradValue =
        this->patchInternalField() + refGrad_/this->patch().deltaCoeffs();

    tmp<Field<Type> > transformGradValue =
        transform(I - valueFraction_, gradValue);

    Field<Type>::operator=(normalValue + transformGradValue);

    transformFvPatchField<Type>::evaluate();
}

7. basicSymmetry

这个类的结构与 directionMixed 类似，对 snGrad ， snGradTransformDiag 和 evaluate 等几个函数进行了重新定义。

snGrad 和 snGradTransformDiag

template<class Type>
Foam::tmp<Foam::Field<Type> >
Foam::basicSymmetryFvPatchField<Type>::snGrad() const
{
    tmp<vectorField> nHat = this->patch().nf();

    const Field<Type> iF(this->patchInternalField());

    return
        (transform(I - 2.0*sqr(nHat), iF) - iF)
       *(this->patch().deltaCoeffs()/2.0);
}

template<class Type>
Foam::tmp<Foam::Field<Type> >
Foam::basicSymmetryFvPatchField<Type>::snGradTransformDiag() const
{
    const vectorField nHat(this->patch().nf());

    vectorField diag(nHat.size());

    diag.replace(vector::X, mag(nHat.component(vector::X)));
    diag.replace(vector::Y, mag(nHat.component(vector::Y)));
    diag.replace(vector::Z, mag(nHat.component(vector::Z)));

    return transformFieldMask<Type>(pow<vector, pTraits<Type>::rank>(diag));
}

evaluate

template<class Type>
void Foam::basicSymmetryFvPatchField<Type>::evaluate(const Pstream::commsTypes)
{
    if (!this->updated())
    {
        this->updateCoeffs();
    }

    tmp<vectorField> nHat = this->patch().nf();

    const Field<Type> iF(this->patchInternalField());

    Field<Type>::operator=
    (
        (iF + transform(I - 2.0*sqr(nHat), iF))/2.0
    );

    transformFvPatchField<Type>::evaluate();
}

另外，值得注意的是，当模板参数 Type 是 scalar 时， snGrad 和 evaluate 函数有其他的定义：

template<>
Foam::tmp<Foam::scalarField>
Foam::basicSymmetryFvPatchField<Foam::scalar>::snGrad() const
{
    return tmp<scalarField >(new scalarField(size(), 0.0));
}

template<>
void Foam::basicSymmetryFvPatchField<Foam::scalar>::evaluate
(
    const Pstream::commsTypes
)
{
    if (!updated())
    {
        updateCoeffs();
    }

    scalarField::operator=(patchInternalField());
    transformFvPatchField<scalar>::evaluate();
}

从这两个函数可推断，当 Type = scalar 时， basicSymmetry 其实就相当于 zeroGradient。

关于 transform 和 transformFieldMask 这两个函数，摸索了很久。前者涉及的源文件有 symmTransformField.C ， transformFieldTemplates.C ；后者的定义在 symmTransformField.H，涉及到的 pow 函数的定义在FieldFunctions.C。此外，这两个函数还需要用到类似 TFOR_ALL_F_OP_FUNC_F_F 的宏，定义在fieldM.H，而这个宏里涉及到的类似 List_ELEM 这样的宏，则定义在 ListLoopM.H。

看了这么多，仍然无法完全确定这两个函数的具体的行为。主要的障碍在于那个 pow 函数实在看不明白。最后只好来对这两个函数进行了一些测试，测试结果总结如下：

1	transform(tensorField p1, vectorField p2)

返回的是另一个 vectorField ，其值等于 p1 与 p2 的内积（即点乘）。注意，一般使用过程中总能保证 p1.size() == p2.size()，但是如果 p1.size() > p2.size()，则返回结果的 size 等于 p2.size() ，值则等于 p1 的前 p2.size() 部分与 p2 的内积。
Boundary Conditions in OpenFOAM 这个 silde 也提到了29页也同样提到了 transform 函数的作用

inline scalar transform(constsymmTensor&, const scalar s)
{
    return s;
}

template<class Cmpt>
inline Vector<Cmpt> transform(const symmTensor& stt, const Vector<Cmpt>& v)
{
    return stt & v;
}

而 transformFieldMask

1	transformFieldMask<Type>(pow<vector, pTraits<Type>::rank>(diag))

目前测试的结果是，其返回值等于 diag 。

有了上面对 transform 和 transformFieldMask 两个函数的测试结果，就可以来分析 basicSymmetry 和 directionMixed 两个边界条件的行为了。

basicSymmetry

对于标量，前面说过其等价于 zeroGradient，所以这里只分析矢量的情形。
从 evaluate 函数，可以得到如下公式
$$
\begin{align}
\overrightarrow{\phi}_b = & \left [\overrightarrow{\phi}_c + (\mathrm{I} - 2\overrightarrow{n} \otimes \overrightarrow{n})\cdot \overrightarrow{\phi}_c \right ] \cdot \frac{1}{2.0} \\
= & \overrightarrow{\phi}_c- \left ( \overrightarrow{\phi}_c \cdot \overrightarrow{n} \right)\cdot \overrightarrow{n}
\end{align}
$$
这意味着，边界上的值等于其邻近网格中心的值的切向分量。
为了方便分析四个系数，将上式写成分量的形式:
$$
\begin{align}
\begin{bmatrix}
\phi_{px} \\
\phi_{py} \\
\phi_{pz}
\end{bmatrix} = &
\begin{bmatrix}
\phi_{cx} \\
\phi_{cy} \\
\phi_{cz}
\end{bmatrix} -
\begin{bmatrix}
(\phi_{cx}n_x + \phi_{cy}n_y + \phi_{cz}n_z)n_x \\
(\phi_{cx}n_x + \phi_{cy}n_y + \phi_{cz}n_z)n_y \\
(\phi_{cx}n_x + \phi_{cy}n_y + \phi_{cz}n_z)n_z
\end{bmatrix} \\
= & \begin{bmatrix}
(1-n_xn_x)\phi_{cx} \\
(1-n_yn_y)\phi_{cy} \\
(1-n_zn_z)\phi_{cz}
\end{bmatrix} -
\begin{bmatrix}
\phi_{cy}n_yn_x + \phi_{cz}n_zn_x \\
\phi_{cx}n_xn_y + \phi_{cz}n_zn_y \\
\phi_{cx}n_xn_z + \phi_{cy}n_yn_z
\end{bmatrix}
\end{align}
$$
照此公式，可以分析得到四个系数如下：
$$
valueInternalCoeffs =
\begin{bmatrix}
(1-n_xn_x) \\
(1-n_yn_y) \\
(1-n_zn_z)
\end{bmatrix}
$$
$$
valueBoundaryCoeffs =
\begin{bmatrix}
\phi_{px} \\
\phi_{py} \\
\phi_{pz}
\end{bmatrix} - valueInternalCoeffs
\begin{bmatrix}
\phi_{cx} \\
\phi_{cy} \\
\phi_{cz}
\end{bmatrix}
$$
$$
gradientInternalCoeffs= - \Delta
\begin{bmatrix}
(n_xn_x) \\
(n_yn_y) \\
(n_zn_z)
\end{bmatrix}
$$
$$
gradientBoundaryCoeffs = - \begin{bmatrix}
(\phi_{cx}n_x + \phi_{cy}n_y + \phi_{cz}n_z)n_x \\
(\phi_{cx}n_x + \phi_{cy}n_y + \phi_{cz}n_z)n_y \\
(\phi_{cx}n_x + \phi_{cy}n_y + \phi_{cz}n_z)n_z
\end{bmatrix} \Delta - gradientInternalCoeffs
\begin{bmatrix}
\phi_{cx} \\
\phi_{cy} \\
\phi_{cz}
\end{bmatrix}
$$

但是，实际上 OpenFOAM 里不是这么实现的！关键就在于这个 snGradTransformDiag 函数的定义与预期不符。
根据我的测试， snGradTransformDiag 函数返回值应该是
$$
snGradTransformDiag =
\begin{bmatrix}
|n_x| \\
|n_y| \\
|n_z|
\end{bmatrix}
$$
即，张量 $\overrightarrow{n}\otimes\overrightarrow{n}$ 的主对角线元素组成的矢量。

而 snGrad 函数的返回值，根据代码可知
$$
snGrad = - \left ( \overrightarrow{\phi}_c \cdot \overrightarrow{n} \right)\cdot \overrightarrow{n}\cdot \Delta
$$
所以，OpenFOAM 中定义的四个系数为：
$$
valueInternalCoeffs =
\begin{bmatrix}
(1-|n_x|) \\
(1-|n_y|) \\
(1-|n_z|)
\end{bmatrix}
$$
$$
valueBoundaryCoeffs =
\begin{bmatrix}
\phi_{px} \\
\phi_{py} \\
\phi_{pz}
\end{bmatrix} - valueInternalCoeffs
\begin{bmatrix}
\phi_{cx} \\
\phi_{cy} \\
\phi_{cz}
\end{bmatrix}
$$
$$
gradientInternalCoeffs= - \Delta
\begin{bmatrix}
|n_x| \\
|n_y| \\
|n_z|
\end{bmatrix}
$$
$$
gradientBoundaryCoeffs = - \begin{bmatrix}
(\phi_{cx}n_x + \phi_{cy}n_y + \phi_{cz}n_z)n_x \\
(\phi_{cx}n_x + \phi_{cy}n_y + \phi_{cz}n_z)n_y \\
(\phi_{cx}n_x + \phi_{cy}n_y + \phi_{cz}n_z)n_z
\end{bmatrix} \Delta - gradientInternalCoeffs
\begin{bmatrix}
\phi_{cx} \\
\phi_{cy} \\
\phi_{cz}
\end{bmatrix}
$$

这里的 $\Delta$ 代表代码中的 deltaCoeffs 。

directionMixed

directionMixed 与 basicSymmetry 是类似的，差别在于 directionMixed 所使用的对称张量是指定的，而不一定是 $\overrightarrow{n}\otimes\overrightarrow{n}$。
根据 evaluate 函数，可以得到如下公式：
$$
\begin{align}
\overrightarrow{\phi}_b = & \overrightarrow{\phi}_{ref}\cdot \mathbf{vF} + (\mathrm{I} - \mathbf{vF}) \cdot \left (\overrightarrow{\phi}_c + \frac{\overrightarrow{G}}{\Delta} \right)\\
= & (\mathrm{I} - \mathbf{vF}) \cdot \overrightarrow{\phi}_c + \overrightarrow{\phi}_{ref}\cdot vF + (\mathrm{I} - \mathbf{vF}) \cdot \frac{\overrightarrow{G}}{\Delta}
\end{align}
$$
其中，$\overrightarrow{\phi}_{ref}=refValue$，$\overrightarrow{G}=refGrad$，$\mathbf{vF}=valueFraction$
同样，为了方便分析，将上述公式的部分写成分量形式：
$$
\begin{align}
\begin{bmatrix}
\phi_{px} \\
\phi_{py} \\
\phi_{pz}
\end{bmatrix} = & \begin{bmatrix}
\phi_{cx} \\
\phi_{cy} \\
\phi_{cz}
\end{bmatrix} - \begin{bmatrix}
vF_{xx}\phi_{cx} + vF_{xy}\phi_{cy} + vF_{xz}\phi_{cz}\\
vF_{yx}\phi_{cx} + vF_{yy}\phi_{cy} + vF_{yz}\phi_{cz} \\
vF_{zx}\phi_{cx} + vF_{zy}\phi_{cy} + vF_{zz}\phi_{cz}
\end{bmatrix} + \overrightarrow{\phi}_{ref}\cdot \mathbf{vF} + (\mathrm{I} - \mathbf{vF}) \cdot \frac{\overrightarrow{G}}{\Delta} \\
= & \begin{bmatrix}
(1-vF_{xx})\phi_{cx} \\
(1-vF_{yy})\phi_{cy} \\
(1-vF_{zz})\phi_{cz}
\end{bmatrix} - \begin{bmatrix}
vF_{xy}\phi_{cy} + vF_{xz}\phi_{cz}\\
vF_{yx}\phi_{cx} + vF_{yz}\phi_{cz} \\
vF_{zx}\phi_{cx} + vF_{zy}\phi_{cy}
\end{bmatrix} + \overrightarrow{\phi}_{ref}\cdot \mathbf{vF} + (\mathrm{I} - \mathbf{vF}) \cdot \frac{\overrightarrow{G}}{\Delta}
\end{align}
$$
同样的，OpenFOAM 中四个系数的实现也与预期的不一样。主要还是 snGradTransformDiag 的定义与预期的不符:
$$
snGradTransformDiag =
\begin{bmatrix}
\sqrt{|vF_{xx}|} \\
\sqrt{|vF_{yy}|} \\
\sqrt{|vF_{zz}|}
\end{bmatrix}
$$

结合代码，可以得到四个系数如下：
$$
valueInternalCoeffs =
\begin{bmatrix}
(1-\sqrt{|vF_{xx}|}) \\
(1-\sqrt{|vF_{yy}|}) \\
(1-\sqrt{|vF_{zz}|})
\end{bmatrix}
$$
$$
valueBoundaryCoeffs =
\begin{bmatrix}
\phi_{px} \\
\phi_{py} \\
\phi_{pz}
\end{bmatrix} - valueInternalCoeffs
\begin{bmatrix}
\phi_{cx} \\
\phi_{cy} \\
\phi_{cz}
\end{bmatrix}
$$
$$
gradientInternalCoeffs= - \Delta
\begin{bmatrix}
\sqrt{|vF_{xx}|} \\
\sqrt{|vF_{yy}|} \\
\sqrt{|vF_{zz}|}
\end{bmatrix}
$$
$$
gradientBoundaryCoeffs = - \mathbf{vF} \cdot \overrightarrow{\phi}_c \cdot \Delta+ \overrightarrow{\phi}_{ref}\cdot \mathbf{vF} \cdot \Delta + (\mathrm{I} - \mathbf{vF}) \cdot \overrightarrow{G} - gradientInternalCoeffs \cdot \overrightarrow{\phi}_c
$$

代码里的 snGrad 函数对应公式为：
$$
\left [ \overrightarrow{\phi}_{ref}\cdot \mathbf{vF} + (\mathrm{I} - \mathbf{vF}) \cdot (\overrightarrow{\phi}_c + \frac{\overrightarrow{G}}{\Delta}) - \overrightarrow{\phi}_c \right ]\cdot \Delta
$$

不知道为什么 snGradTransformDiag 要按照这种方式来定义，可能是为了数值稳定性。不过，由于 valueBoundaryCoeffs 和 gradientBoundaryCoeffs 分别是在 valueInternalCoeffs 和 gradientInternalCoeffs 的基础之上定义的，所以总是能保证 evaluate 的结果与预期一致。

可以将 directionMixed 的行为总结如下：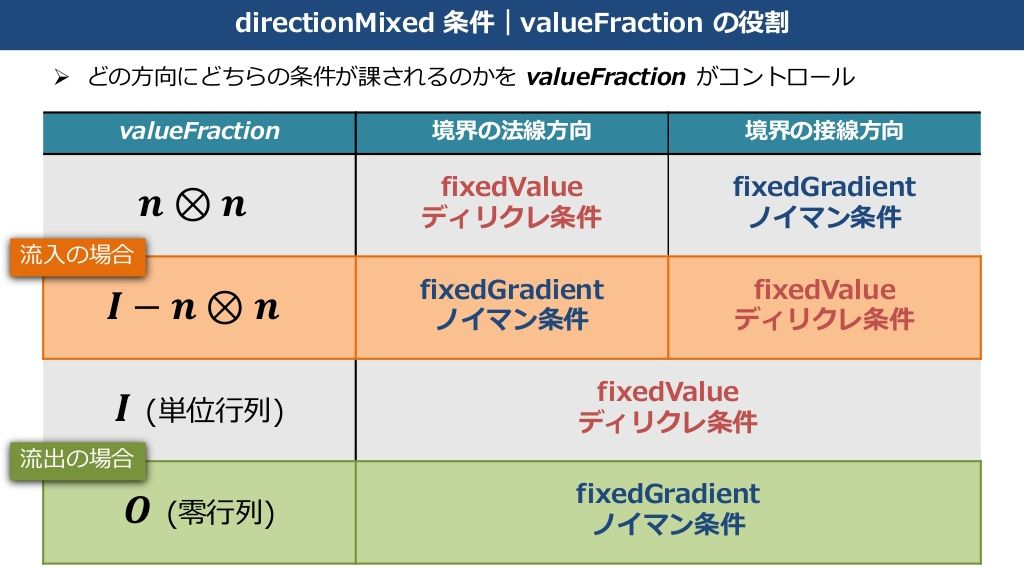
directionMixed 的行为

不过，如果 valueFraction 的值是任意指定的，而不是由 $\overrightarrow{n}\otimes\overrightarrow{n}$ 构成的，那又另当别论了。

参考资料：
Boundary Conditions in OpenFOAM

Giskard's CFD Learning Tricks

CFD and Scientific Computing